不是VIP会员,不能显示答案
1350 【入门】纸盒的最大体积是多少?
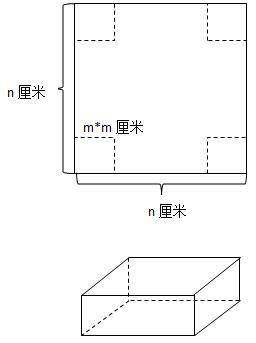
| 题目描述: | 在一张尺寸为n * n厘米的正方形硬纸板的四个角上,分别裁剪掉一个m * m厘米的小正方形,就可以做成一个无盖纸盒,请问这个无盖纸盒的最大体积是多少? (立方体的体积v = 底面积 * 高) 比如:n = 5,那么裁掉的小正方形的尺寸可能是1厘米、2厘米 如果裁掉1厘米的四个小正方形,得到纸盒的体积 = (5 - 2) * (5 - 2) * 1 = 9立方厘米 如果裁掉2厘米的四个小正方形,得到纸盒的体积 = (5 - 4) * (5 - 4) * 2 = 2立方厘米 因此,裁掉边长为2的四个小正方形得到的纸盒体积最大,最大体积为9(立方厘米) (7.1)
|
| 输入: | 一个整数n,代表正方形纸板的边长 |
| 输出: | 纸盒的最大体积 |
| 样例输入: | 5 |
| 样例输出: | 9 |
| 提示: | |
| 来源: | 需要找规律的循环 |
| 解答: | 需要找规律的循环 |